Terminy sierpniowych egzaminów poprawkowych w roku szkolnym 2022/2023

 

25 sierpnia godzina 10:00 - język angielski (klasa4)

28 sierpnia godzina 9:00 - język angielski (pozostałe klasy)

29 sierpnia godzina 9:00 - matematyka 

30 sierpnia godzina 9:00 - język polski, język niemiecki, geografia, 

                   godzina 10:00 - chemia, język migowy 

 

Zagadnienia do sierpniowych egzaminów poprawkowych w roku szkolnym 2022/2023

 

MATEMATYKA

KLASA   I 

LICZBY

• działania w zbiorze liczb rzeczywistych, z uwzględnieniem działań na potęgach i pierwiastkach
• obliczanie logarytmów z definicji
• uwalnianie niewymierności z mianownika ułamka
• wyrazy podobne i ich redukcja
• wzory skróconego mnożenia: kwadrat sumy, kwadrat różnicy, różnica kwadratów
• działania na wyrażeniach algebraicznych

RÓWNANIA I NIERÓWNOŚCI

• równania i nierówności liniowe z zastosowanie wzorów skróconego mnożenia
• algebraiczne rozwiązywanie układów równań liniowych
• zaznaczanie przedziałów liczbowych na osi liczbowej, z uwzględnieniem działań na przedziałach
• podstawowe równania i nierówności z wartością bezwzględną
• definicja procentu i obliczenia procentowe
• zastosowanie obliczeń procentowych do rozwiązywania zadań tekstowych
• definicja funkcji
• wyznaczanie dziedziny funkcji i miejsca zerowego
• odczytywanie własności funkcji na podstawie wykresu
• wykres i własności funkcji liniowej

               FUNKCJA LINIOWA

• definicja funkcji liniowej i jej wykres
• wyznaczanie wzoru funkcji liniowej, której wykres przechodzi przez dwa dane punkty
• wyznaczanie wzoru funkcji, której wykres jest równoległy, prostopadły do danej funkcji i przechodzi przez dany punkt
• obliczanie miejsca zerowego , określanie przedziałów  monotoniczność i przedziałów tych argumentów,  dla których funkcja liniowa przyjmuje wartości dodatnie , ujemne.
• algebraiczne i geometryczne rozwiązywanie układów równań liniowych

 

KLASA   II

 

• wyznaczanie dziedziny funkcji
• obliczanie miejsca zerowego
• odczytywanie własności funkcji na podstawie wykresu

               FUNKCJA LINIOWA

• definicja funkcji liniowej i jej wykres
• wyznaczanie wzoru funkcji liniowej, której wykres przechodzi przez dwa dane punkty
• wyznaczanie wzoru funkcji, której wykres jest równoległy, prostopadły do danej funkcji i przechodzi przez dany punkt
• obliczanie miejsca zerowego , określanie przedziałów  monotoniczność i przedziałów tych argumentów,  dla których funkcja liniowa przyjmuje wartości dodatnie , ujemne.
• algebraiczne i geometryczne rozwiązywanie układów równań liniowych

                FUNKCJA KWADRATOWA !!!

• postać kanoniczna f.kwadrat., współrzędne wierzchołka paraboli
• postać ogólna f.kwadrat.
• postać iloczynowa f.kwadrat.
• obliczanie wyróżnika i miejsc  zerowych
• równania i nierówności kwadratowe
• wykres i własności f. kwadratowej

               WIELOMIANY

• pojęcie wielomianu, jego stopień i pierwiastek
• działania na wielomianach
• rozkładanie wielomianów na czynniki (wszystkie metody)
• równania wielomianowe

               WYRAŻENIA WYMIERNE

• dziedzina wyrażeń wymiernych
• działania na wyrażeniach wymiernych
• równania wymierne

GEOMETRIA PŁASKA I TRYGONOMETRIA

• kąty w kole
• twierdzenie Talesa
• funkcje trygonometryczne kąta ostrego i rozwartego
• zastosowanie funkcji trygonometrycznych w obliczaniu pól i obwodów figur płaskich

 

KLASA   III 

GEOMETRIA PŁASKA I TRYGONOMETRIA

• kąty w kole
• twierdzenie Talesa
• funkcje trygonometryczne kąta ostrego i rozwartego
• zastosowanie funkcji trygonometrycznych w obliczaniu pól i obwodów figur płaskich

FUNKCJA WYKŁADNICZA I POTĘGOWA

• potęga o wykładniku rzeczywistym
• działania na potęgach o wykładniku rzeczywistym
• definicja logarytmu
• obliczanie logarytmów liczby na podstawie definicji
• obliczanie wartości wyrażeń zawierających logarytmy z zastosowaniem poznanych twierdzeń na logarytmach

( tw. o sumie logarytmów, tw. o różnicy logarytmów, tw. o logarytmie potęgi)

• definicja funkcji wykładniczej i logarytmicznej oraz  ich wykresy

 

GEOMETRIA ANALITYCZNA

• równanie prostej w postaci ogólnej i kierunkowej
• długość i środek odcinka
• równania prostej prostopadłej do danej prostej, prostej równoległej do danej prostej
• odległość punktu od prostej
• równanie okręgu

 

CIĄGI LICZBOWE

• wyznaczanie wyrazów ciągu, wzoru na wyraz ogólny ciągu liczbowego
• wyznaczanie wyrazów ciągu arytmetycznego
• zależność między trzema kolejnymi wyrazami ciągu arytmetycznego
• wyznaczanie sumy n- początkowych wyrazów ciągu arytmetycznego
• wyznaczanie wyrazów ciągu geometrycznego
• zależność między trzema kolejnymi wyrazami ciągu geometrycznego
• wyznaczanie sumy n- początkowych wyrazów ciągu geometrycznego

 

KLASA   IV

• równania i nierówności kwadratowe
• równania wielomianowe w postaci iloczynowej
• równania wymierne
• ciąg arytmetyczny
• pola i objętość graniastosłupów prostych

PRZYKŁADOWE ZADANIA

Zad. 1    Rozwiąż nierówność kwadratową: - 2x² - 6x > -8.

Zad. 2    Rozwiąż równanie (3x-2)(5x²-2x)(x²-3)=0.

Zad. 3   Rozwiąż równanie:

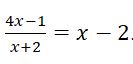
Zad. 4    Wyznacz wzór na wyraz ogólny ciągu arytmetycznego wiedząc, że: a₃=-5, a₆=1. Oblicz sumę 12-tu początkowych wyrazów tego ciągu.

Zad. 5   Oblicz objętość i pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego o danych: krawędzi podstawy 5 i przekątnej ściany bocznej 13.

 

GEOGRAFIA

KLASA  I

KARTOGRAFIA

• Źródła informacji geograficznej
• Metody badań geograficznych
• Mapa jako obraz Ziemi
• Metody prezentowania informacji na mapach
• Odczytywanie informacji z mapy
• Obliczanie odległości, przeliczanie skali 
• Geograficzne systemy informacyjne

ATMOSFERA

• Budowa atmosfery
• Temperatura powietrza
• Ciśnienie atmosferyczne
• Opady atmosferyczne
• Prognozowanie pogody i ekstremalne zjawiska pogodowe
• Czynniki klimatotwórcze
• Klimaty kuli ziemskiej

Mapa fizyczna oraz polityczna Europy i Azji.

JĘZYK ANGIELSKI 

KLASA II   
                        

Podręcznik: Checkpoint B1+

Rozdział 5 
gramatyka: czasowniki modalne (should, must, have to ...); zdania warunkowe typ I i II; słownictwo: przedmioty nauczania; oceny i wymagania

Rozdział 6 
gramatyka: strona bierna; have sth done; 
słownictwo: urządzenia techniczne; obsługa i korzystanie z urządzeń technicznych; wyrażenia przyimkowe.

Rozdział 7
gramatyka: zaimki względne (which/ who / where / when / whose) 
słownictwo: dyscypliny sportu, obiekty sportowe; sprzęt sportowy, uprawianie sportu

Rozdział 8
gramatyka: mowa zależna (zdania oznajmujące, przeczące, pytające, rozkazy, zakazy)
słownictwo: dziedziny kultury, twórcy i ich dzieła; przymiotniki z końcówką  „-ing” / „-ed”

Rozdział 9
gramatyka: czasowniki modalne wyrażające przeszłość ( must have / could have / might have … ); zadania warunkowe typ III
słownictwo: struktura państwa

Rozdział 10
gramatyka: zaimki something / anything / everything / someone / somewhere … ; so / such; 
I wish … / If only ...
słownictwo: rodzaje sklepów; sprzedawanie, kupowanie; zaimki z money

Podręcznik B2 / Rozdział 1
gramatyka: czasy Present Simple / Present Continuous / Present Perfect / Present Perfect Continuous

 

KLASA  IIIA
                
Podręcznik: Checkpoint B2

Rozdział 5
gramatyka: czasowniki modalne (should, must, have to …) wyrażając teraźniejszość, przyszłość i przeszłość.
słownictwo: sprzedawanie i kupowanie, środki płatnicze; korzystanie z usług bankowych, finanse; czasowniki frazowe

Rozdział 6 
gramatyka: zdania warunkowe 0, 1, 2, 3 wraz z unless, as long as, providing, in case … ; I wish … / If only...  wyrażając teraźniejszość i przeszłość
słownictwo: części ciała; tryb życia, choroby, ich objawy i leczenie

Rozdział 7
gramatyka: mowa zależna (zdania oznajmujące, przeczące, pytające, rozkazy, zakazy)
słownictwo: dziedziny kultury / twórcy i ich dzieła; rzeczowniki złożone; przymiotniki złożone

Rozdział 8
gramatyka: strona bierna
słownictwo: klęski żywiołowe; czasowniki z przyimkami

Rozdział 9
gramatyka: gerunds / infinitives – stosowanie odpowiedniej formy czasownika / zmiana znaczenia zdania z czasownikami stop, remember, forget, like
słownictwo: urządzenia techniczne; obsługa i korzystanie z podstawowych urządzeń technicznych; czasowniki frazowe

Rozdział 10
gramatyka: zdania warunkowe mieszane; indirect questions (pytania pośrednie); question tags 
słownictwo: media

 

KLASA 3B

Słownictwo –      repetytorium rozdziały 1,2,3

                             Czasowniki nieregularne

Gramatyka -        Czasy: Present Simple, Present Continuous, Past Simple, Past Continuous

                            Question tags

                            Strona Bierna

Mówienie -         opis obrazka, opowiadanie o sobie oraz o wydarzeniach przeszłych

 

KLASA 4

Słownictwo –    repetytorium rozdziały 6,7,8,9,10

                           Czasowniki nieregularne

Gramatyka –     Zdania warunkowe typ 1,2,3

                           Czasy: Present Simple, Present Continuous, Past Simple, Past Continuous

                           Strona Bierna

Mówienie -        opis obrazka, opowiadanie o sobie oraz o wydarzeniach przeszłych

INFORMATYKA

KLASA II

Pytania:

1. Grafika wektorowa vs grafika rastrowa - definicje, różnice, wady, zalety, programy
2. Popularne formaty zapisu plików video - wymienić, opisać, podać wady, zalety.
3. Do czego odnoszą się skróty H.264 i H.265. Jakich plików dotyczą, jaka jest między nimi różnica.
4. Jaki wpływ na komórkę z danymi w arkuszu kalkulacyjnym będzie miało dopisanie do obydwu współrzędnych tej komórki znacznika $?
5. Czy arkusz kalkulacyjny jest bazą danych?
6. ULC - Podstawowe zasady lotów w kategorii otwartej

Zadania:

1. Wygeneruj, w dostępnym na pulpicie programie do obróbki video, 30 sekundowy film złożony z min. 3 ujęć, zawierający efekty przejść między ujęciami, oraz ścieżkę dźwiękową. Na pierwszym ujęciu umieść napis “Egzamin”, znikający po 5 sekundach. Pliki do wykorzystania znajdują się na pulpicie w folderze: “egzamin klasyfikacyjny”. Gotowy plik zapisz w formacie mp4, FHD.
2. W arkuszu kalkulacyjnym stwórz wykres funkcji y=1/x oraz tabelę z danymi niezbędnymi do otrzymania tego wykresu. Dane x powinny zawierać się w zakresie 1-100, zmiana co 0,5. Wykres powinien składać się z minimum 200 punktów pomiarowych. 
3. W arkuszu kalkulacyjnym przygotuj arkusz służący do prowadzenia rejestru wejść/wyjść pracowników firmy. Dane powinny zawierać min. 3 pracowników, imię nazwisko pracownika, godzinę wejścia, godzinę wyjścia, czas pracy. W przypadku czasu pracy wynoszącego mniej niż 8h, komórka powinna zmienić kolor tła na czerwony

CHEMIA

KLASA I

1. Budowa atomu- protony, elektrony, neutrony.
2. Liczba atomowa i masowa.
3. Izotopy wodoru.
4. Konfiguracja elektronowa, konfiguracja powłokowa i konfiguracja skrócona atomów od liczby atomowej 1 do 20.
5. Wiązania jonowe w cząsteczce soli kuchennej.
6. Wiązanie kowalencyjne spolaryzowane w cząsteczce HCl.
7. Wiązania kowalencyjne niespolaryzowane w cząsteczkach wodoru, tlenu i azotu.
8. Elektrony walencyjne.
9. Budowa Układu Okresowego Pierwiastków.
10. Obliczanie stosunku atomowego, masowego i procentowego atomów w związku chemicznym.
11. Obliczanie masy cząsteczkowej związku chemicznego.
12. Obliczanie masy mola substancji.
13. Obliczanie masy molowej substancji.
14. Rodzaje mieszanin.
15. Roztwory właściwe, koloidalne i zawiesiny.
16. Metody rozdzielania mieszanin.
17. Rozpuszczalność substancji – analiza wykresów zależności rozpuszczalności od temperatury.

KLASA II

1.Równania dysocjacji jonowej kwasów, zasad i soli.

2.Nazewnictwo jonów.

3.Odczyn wodny roztworu.

4.Skala pH.

5.Wskaźniki odczynu roztworu.

6. Zapis cząsteczkowy, jonowy i jonowy skrócony reakcji zobojętniania.

7. Szybkość reakcji – wzór, jednostka.

8. Czynniki wpływające na szybkość reakcji.

9.Reakcje egzo i endoenergetyczne.

10.Kataliza.

11. Wyznaczanie stopni utlenienia atomów w związkach chemicznych.

12.Reakcje erdoks – proces utleniania i redukcji, bilans elektronowy.

13.Budowa ogniwa Daniella.

14.Korozja stali w różnych warunkach.

15. Budowa, nazewnictwo i otrzymywanie tlenków, wodorotlenków kwasów tlenowych i beztlenowych oraz soli.

16.Wykrywanie węglanu wapnia.

17.Wykrywanie dwutlenku węgla.

18.Zaprawa murarska.

19.Zjawiska krasowe.

20. Twardość wody.

21. Gips krystaliczni i gips palony – hydraty.

22. Zaprawa gipsowa.

23.Rodzaje szkła.

 

KLASA III

1.Alkohole – wzory sumaryczne, półstrukturalne i strukturalne, nazewnictwo, otrzymywanie i rzędowość.

2.Aldehydy i ketony– wzory sumaryczne, półstrukturalne i strukturalne, nazewnictwo, otrzymywanie.

3.Kwasy karboksylowe– wzory sumaryczne, półstrukturalne i strukturalne, nazewnictwo, otrzymywanie.

4.Estry– wzory sumaryczne, półstrukturalne i strukturalne, nazewnictwo.

5.Reakcja estryfikacji.

6.Aminy– wzory sumaryczne, półstrukturalne i strukturalne, nazewnictwo, rzędowość.

7.Aminokwasy– wzory sumaryczne, półstrukturalne i strukturalne, nazewnictwo.

8.Aminokwasy biogenne – glicyna i alanina.

9.Wiązanie peptydowe – budowa.

10.Monosacharydy – glukoza i fruktoza.

11.Disacharydy – maltoza i sacharoza.

12.Wiązanie glikozydowe.

13.Fermentacja alkoholowa.

14.Fermentacja octowa.

15. Fermentacja mlekowa.

16.Fermentacja masłowa.

JĘZYK POLSKI

KLASA 1

ANTYK

• Pojęcie mitu, przykłady mitów, funkcje, podstawowe rodzaje mitów.
• Jak, wg mitologii greckiej, powstał świat, bogowie, ludziea) „genealogia” bogów greckich
•  najważniejsi bogowie greccy (czym się zajmowali i jakie były ich cechy)
•  archetypy i toposy ważne dla kultury europejskiej (np. topos labiryntu, wędrówki, Arkadii, archetyp władcy, wojownika, matki itp.)
• Przedstawienie historii wybranych bohaterów mitologicznych ( np. Prometeusza, Syzyfa, Narcyza, Dedala, Ikara )
• „Antygona” Sofoklesa
• a) początki teatru greckiego
• b) cechy tragedii antycznej
• c) podstawowe pojęcia związane z tragedią antyczną (fatum, tragedia, tragizm, ironia tragiczna, katharsis) 
• d) budowa tragedii antycznej 
• e) przedstawienie treści „Antygony” w kontekście mitu o rodzie Labdakidów
• f) konflikt Antygony z Kreonem 
• g) charakterystyka postaci dramatu
•  Horacjańska koncepcja artysty.

• Filozofia antyczna: stoicyzm, epikureizm, horacjanizm.

BIBLIA

•  
•  Podstawowe wiadomości na temat Biblii (pochodzenie, budowa, Stary i Nowy Testament, księgi biblijne, gatunki biblijne).
• Postaci bohaterów biblijnych oraz najważniejsze biblijne motywy.
• Religijna i kulturotwórcza rola Biblii.
• Biblijny opis stworzenia świata.
• Podstawowe wiadomości o Księdze Psalmów ( autorstwo, rodzaje psalmów, przekłady na język polski).
• Problem cierpienia człowieka ukazany w Księdze Hioba. Znajomość historii Hioba.
• Wizja końca świata i Sądu Ostatecznego ukazana w Apokalipsie św. Jana.

ŚREDNIOWIECZE

•  Etymologia nazwy epoki, najważniejsze wydarzenia związane z początkiem i końcem średniowiecza.
• Znaczenie pojęć: „uniwersalizm” i „teocentryzm”.
• Wzorce osobowe popularne w średniowieczu (asceta, rycerz, władca) w odniesieniu do poznanych utworów.
• Analiza wizerunku Śmierci i jej charakterystyka na podstawie „Rozmowy Mistrza Polikarpa ze Śmiercią” ( motyw danse macabre).
• Wizerunek średniowiecznego rycerza w oparciu o „Pieśń o Rolandzie”
• Obraz Matki Boskiej ukazany w „Bogurodzicy” ( motyw deesis) .
• Obraz Matki Boskiej ukazany w „Lamencie świętokrzyskim” ( motyw Stabat Mater).
• Losy bohatera „Legendy o św. Aleksym” ( święty jako asceta)
• Pojęcia : ars moriendi, literatura parenetyczna, anonimowość, hagiografia, historiografia.

RENESANS

• Najważniejsze informacje o epoce: nazwa i ramy czasowe.
• Znaczenie pojęć: „ antropocentryzm”, „humanizm”, „reformacja”.
• Obraz Boga, świata i człowieka jaki wyłania się z Hymnu Jana Kochanowskiego (Czego chcesz
• od nas Panie)
• „Pieśni” Jana Kochanowskiego:
• a)  „Pieśń XX” ( Księgi pierwsze), „Pieśń IX” (Księgi pierwsze), „Pieśń IX” (Księgi wtóre) – recepta poety na życie szczęśliwe, nawiązanie do filozofii starożytnej, rola Boga i Fortuny w życiu człowieka, postawa człowieka wobec losu).
• b)  „Pieśń o spustoszeniu Podola” – przykładem pieśni patriotycznej (sytuacja ukazana w wierszu, obraz/określenie wroga, apel do szlachty polskiej).
• Fraszki Jana Kochanowskiego:
• „Treny” Jana Kochanowskiego:
• a)  kontekst biograficzny „Trenów”, kreacja podmiotu lirycznego
• b)  cechy gatunkowe trenu, nowatorstwo trenów J. Kochanowskiego
• c)  obraz Urszulki w „Trenach”
• d)  rozczarowanie poety filozofią stoicką w Trenie IX, X i XI
• e)  mądrość przedstawiona w Trenie IX
• Obowiązki władzy wobec poddanych na podstawie „Odprawy posłów greckich”.
• Charakterystyka Antenora i Aleksandra.

BAROK

• Znajomość treści Makbeta Szekspira i Skąpca Moliera

JĘZYK NIEMIECKIKI

KLASA I

Gramatyka:

• Odmiana czasowników regularnych, posiłkowych (haben i sein), modalnych, rozdzielnie złożonych
• Odmiana czasowników regularnych, których temat kończy się na: S, B, z
• Odmiana czasowników regularnych, których temat kończy się na: t, d, chn
• Szyk zdania oznajmującego
• Pytania: przez zaimek pytający i przez inwersję
• Rodzajniki określone i nieokreślone w I, III i IV przypadku
• Przeczenie „kein” w I i IV przypadku
• Przeczenie „nicht”
• Zaimki dzierżawcze w mianowniku
• Szyk prosty i przestawny
• Spójniki: denn, aber, oder, und

Leksyka:

• Powitania i pożegnania
• Kraje i stolice krajów niemieckojęzycznych
• Słownictwo związane z opisywaniem samopoczucia
• Liczebniki od 0 do 1000
• Członkowie rodziny
• Opis osoby (imię, wiek, skąd pochodzi, gdzie mieszka, jakie ma hobby)
• Zwierzęta
• Przymiotniki opisujące zwierzęta
• Zawody
• Cechy charakteru
• Czas zegarowy
• Przedmioty szkolne
• Przybory szkolne
• Kolory
• Produkty spożywcze
• Pory dnia
• Smaki
• Typy budynków
• Nazwy pomieszczeń
• Nazwy mebli
• Nazwy sprzętów kuchennych

KLASA III

Gramatyka:

• Czas przeszły Perfekt
• Czas przeszły Praeteritum czasowników modalnych
• Określenie miejsca wo? Wohin? W powiązaniu z opisem miejsc pobytu w czasie wakacji (jestem nad morzem, jadę nad morze – tabelka w zeszycie)
• Zdania okolicznikowe czasu z als i wenn
• Odmiana przymiotnika po rodzajniku nieokreślonym w I i IV przypadku
• Odmiana rzeczownika w dopełniaczu
• Zdania okolicznikowe celu ze spójnikiem damit oraz konstrukcją um…zu
• Szyk zdania po spójnikach: deshalb, sonst, trotzdem
• Przyimki łączące się z III lub IV przypadkiem
• Rekcja czasowników
• Rekcja przymiotników
• Pytanie o dopełnienie przyimkowe
• Zdania względne z zaimkiem pytającym wo
• Konstrukcja bezokolicznikowa z zu i bez zu

Leksyka:

• Opis dnia
• Środki transportu
• Pogoda
• Pory roku
• Miesiące
• Części garderoby (opis osoby)
• Sporty zimowe i letnie
• Kupowanie odzieży
• Wymarzony zawód
• Emocje i uczucia